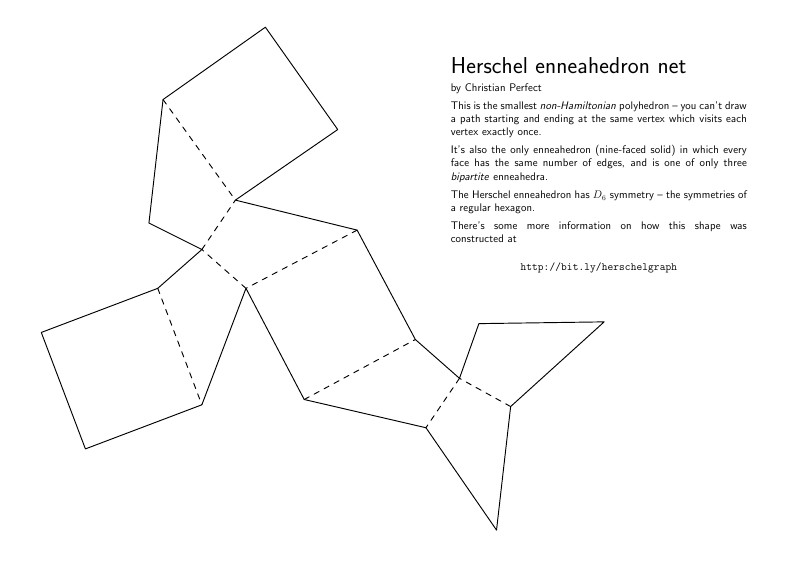
Herschel enneahedron net
Letzte Aktualisierung:
vor 12 Jahren
Lizenz:
Other (as stated in the work)
Abstrakt:
Herschel enneahedron net

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.
%\title{Herschel enneahedron net}
% Herschel enneahedron net, by Christian Perfect 2013.
% With Dr Michael White and Yameng Ji
\documentclass[10pt]{article}
\usepackage{pgf,tikz}
\usepackage[hidelinks]{hyperref}
\usepackage{relsize}
\usepackage[margin=1cm,landscape,paper=a4paper]{geometry}
\usetikzlibrary{arrows}
\usetikzlibrary{calc}
\tikzset{fontscale/.style = {font=\sffamily \relsize{#1}}}
\pagestyle{empty}
\begin{document}
\begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=6.6cm,y=6.6cm,font=\sffamily]
\draw [line width=1pt]
(0.25,-0.66) -- (-0.41,-0.91) -- (-0.66,-0.25) --
(0,0) -- (0.25,0.22) -- (-0.05,0.37) --
(0.03,1.07) -- (0.61,1.48) -- (1.02,0.9) --
(0.44,0.5) -- (1.13,0.33) -- (1.46,-0.29) --
(1.71,-0.51) -- (1.82,-0.2) -- (2.53,-0.19) --
(2,-0.67) -- (1.92,-1.37) -- (1.52,-0.79) --
(0.83,-0.63) -- (0.5,0) -- (0.25,-0.66);
\draw [line width=1pt,dash pattern=on 6pt off 6pt] (0.5,0)-- (0.25,0.22);
\draw [line width=1pt,dash pattern=on 6pt off 6pt] (0,0)-- (0.25,-0.66);
\draw [line width=1pt,dash pattern=on 6pt off 6pt] (1.13,0.33)-- (0.5,0);
\draw [line width=1pt,dash pattern=on 6pt off 6pt] (0.25,0.22)-- (0.44,0.5);
\draw [line width=1pt,dash pattern=on 6pt off 6pt] (0.83,-0.63)-- (1.46,-0.29);
\draw [line width=1pt,dash pattern=on 6pt off 6pt] (0.03,1.07)-- (0.44,0.5);
\draw [line width=1pt,dash pattern=on 6pt off 6pt] (1.71,-0.51)-- (1.52,-0.79);
\draw [line width=1pt,dash pattern=on 6pt off 6pt] (2,-0.67)-- (1.71,-0.51);
\node at (2.5,0.7) [fontscale=1] {\begin{minipage}{0.4\textwidth}
\setlength{\parskip}{1ex}
{\Huge Herschel enneahedron net}
by Christian Perfect
This is the smallest \textit{non-Hamiltonian} \mbox{polyhedron} -- you can't draw a path starting and ending at the same vertex which visits each vertex exactly once.
It's also the only enneahedron (nine-faced solid) in which every face has the same number of edges, and is one of only three \textit{bipartite} enneahedra.
The Herschel enneahedron has $D_6$ symmetry -- the symmetries of a regular hexagon.
There's some more information on how this shape was \mbox{constructed} at
\begin{center}
\mbox{\url{http://bit.ly/herschelgraph}}
\end{center}
\end{minipage}
};
\end{tikzpicture}
\end{document}