LaTeX templates and examples — Math
Kürzlich

This template provides a framework and example for portfolio submissions for students at Grand Valley State University who are in Professor Wells' Math 210 classes.

Document describing basic economic and statistical analysis and how to apply them to machine learning

When an issue arises in a building, people's evacuation is a recurring challenge. We wondered whether we could make a realistic simulation of people’s evacuation based on a simple physical model. First, we elaborated this model and then we simulate the people’s comportment on MATLAB. We could conclude that our simulation is enough to describe the general comportment of people.
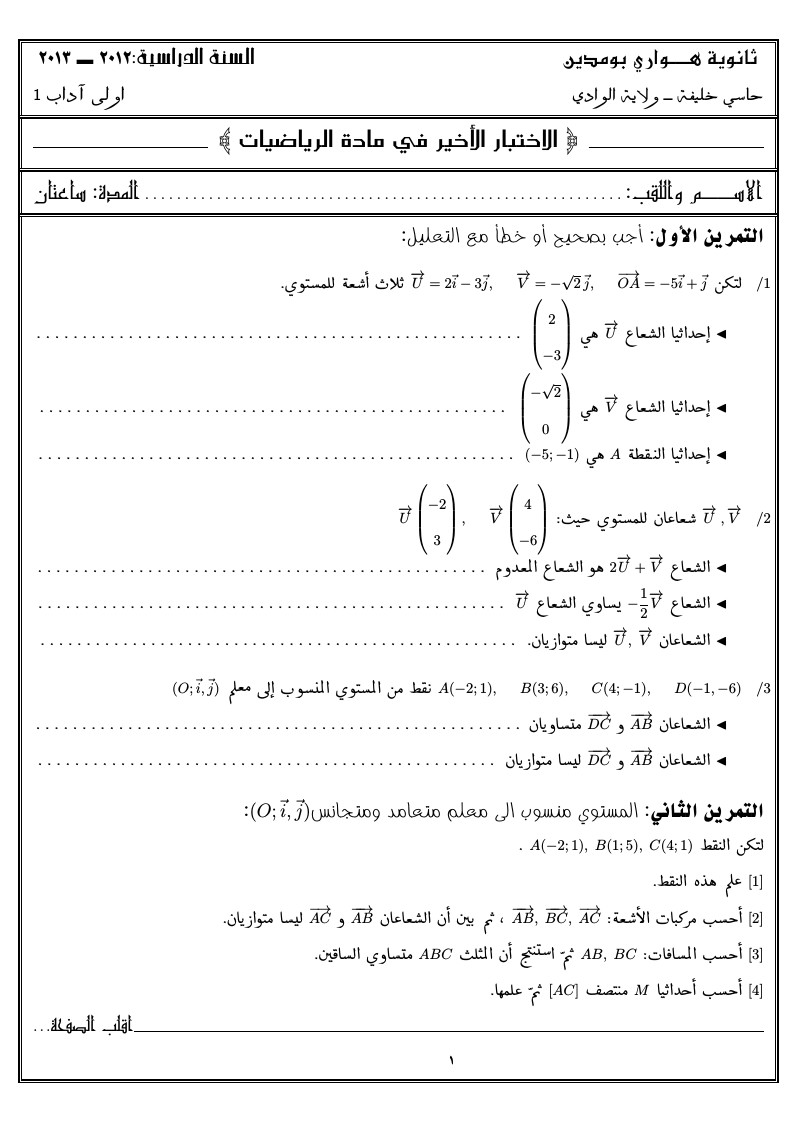
the sujet compiler ( xetex)

A Sample Portfolio/Portfolio Template for use in Dr. Clark Wells's Winter 2015 sections of MTH 210 at Grand Valley State University.

Solving the physics problems you are presented with in an introductory course become easier if each time you sit down to solve a problem, you follow a generalized problem-solving strategy that includes sketching pictures.

Template for the class practice 3.

Man kann die Punkte für jede Aufgabe in einen Array eingeben und sie werden automatisch als Tabelle auf dem Deckblatt angezeigt 🤯 Sieht auch sonst schick aus und enthält viele hilfreiche Makros in der `mathmacros.tex`. Die Vorlage wird als Public Domain ohne Garantie veröffentlicht.

Homework template for SMCM PHYS 251 Fundamentals of Physics 3 (Fun 3). Includes the Griffiths "script-r" used in many electricity and magnetism courses.
\begin
Discover why over 20 million people worldwide trust Overleaf with their work.